Wiskunde
Volledige tweedegraadsvergelijking met 1 onbekende oplossen d.m.v. som en product
Tine krijgt in deze video hulp van SeP bij het berekenen van een 2de graadsvergelijking. (2de graad)
Welkom bij WeZooz Academy
Je bekijkt een gratis preview van deze lesvideo.
Meld je aan, probeer gratis om meer te zien of koop meteen toegang.
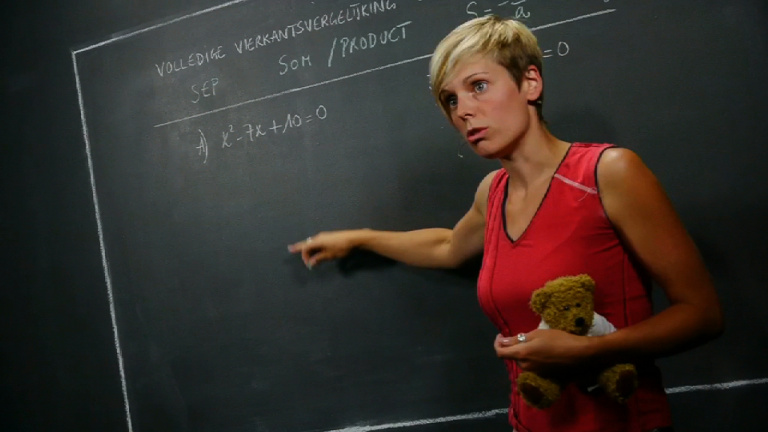
Een volledige tweedegraadsvergelijking met 1 onbekende oplossen: som en product.
WAAROVER GAAT DEZE VIDEO IVM 2DE GRAADSVERGELIJKINGEN?
In deze video verdiept Tine zich in het oplossen van een volledige tweedegraadsvergelijking met 1 onbekende met behulp van de som en het product.
HOE LOS JE EEN 2DE GRAADSVERGELIJKING MET ÉÉN ONBEKENDE OP?
Je kan een volledige tweedegraadsvergelijking met 1 onbekende niet alleen oplossen met behulp van de discriminant. Ook aan de hand van de som en het product van de uitkomsten van de vierkantsvergelijkingen of tweedegraadsvergelijkingen kan het.
De som en het product daarvan is altijd gelijk aan een zelfde formule. Lees deze nog eens na in dit handige schema. Dan is het gewoon invullen en uitrekenen. Dan moet je 2 getallen vinden waarvan het product bijvoorbeeld 10 is, maar waarvan de som ook gelijk is aan bijvoorbeeld 7. Die 2 getallen zijn x1 en x2 en dus de 2 oplossingen die we zoeken. Vergeet je oplossingenverzameling niet te noteren. De SeP-methode ga je vooral gebruiken bij de makkelijke oefeningen.
ZIJN ER NOG VIDEO'S OVER 2DE GRAADSVERGELIJKINGEN?
Wil je meer video's over tweedegraadsvergelijkingen, check dan ook deze video.
