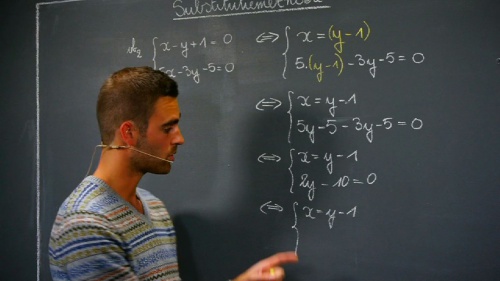Welkom bij het overzicht van stelsels. In drie lestrajecten legt Sjoert uit hoe je stelsels van eerstegraadsvergelijkingen oplost. In totaal maak je met vier methoden kennis om deze wiskundige materie te berekenen. Daarnaast leer je ook vraagstukken oplossen aan de hand van een stelsel. Dankzij de hulp van WeZooz Academy en zijn leerkrachten is elk lesonderwerp in een mum van tijd zo helder als pompwater. Voor wie nog nooit pompwater van dichtbij heeft gezien: maak je dan maar klaar voor een namiddagje herinneringen bij de grootouders. Zij zullen met plezier vertellen hoe helder hun pompwater eruit zag.

Wat kom je te weten i.v.m. stelsels?

Zoals eerder aangegeven, komen er vier methoden aan bo(r)d om stelsels van eerstegraadsvergelijkingen op te lossen. Om precies te weten te komen hoe welke methode precies in elkaar zit, bekijk je natuurlijk de lesvideo’s. We sommen ze hier wel even kort op, maar voor de volledige uitleg en oefeningen klik je op het juiste lestraject.

Welke methodes voor stelsels zijn er?

 Sjoert legt je vier methoden uit om stelsels van eerstegraadsvergelijkingen op te lossen. De bedoeling is altijd dezelfde: je moet de waarde berekenen voor x en y.  

Stelsel van twee eerstegraadsvergelijkingen oplossen – grafisch.

In deze lesvideo legt Sjoert uit hoe je de oplossing van twee eerstegraadsvergelijkingen kan vinden door ze grafisch te berekenen. Door je twee vergelijkingen om te zetten in twee rechten kan je aan de hand van de coördinaten van het gemeenschappelijk snijpunt uitmaken wat de oplossing is.

Stelsel van twee eerstegraadsvergelijkingen oplossen – substitutie.

Hier ga je niet grafisch te werk, maar hervorm je de vergelijkingen telkens weer tot je de oplossing hebt gevonden. Aan de hand van substitutie kan je zo de waarde voor x en y berekenen. Vergeet niet de waarden achteraf op de juiste manier nog eens op te schrijven.  

Stelsel van twee eerstegraadsvergelijkingen oplossen – combinatie.

Hier ga je eerst de waarde van x berekenen door de twee eerstegraadsvergelijkingen met elkaar te combineren. Daarna ga je aan de hand van substitutie de waarde voor y berekenen. Heel belangrijk dus om manier van substitutie in het achterhoofd te houden.

Stelsel van twee eerstegraadsvergelijkingen oplossen – combinatie – puur.

Hier is van substitutie geen sprake meer. Nu ga je de twee eerstegraadsvergelijkingen tweemaal met elkaar combineren (optellen). De eerste keer om de waarde van x te berekenen en de andere keer om de waarde van y te vinden.  

Wat is belangrijk bij het uitrekenen van een stelsel van twee eerstegraadsvergelijkingen?

Vergeet nooit, maar dan ook nooit om de oplossingenverzameling te schrijven. Dit doe je nadat je x en y hebt berekend. De schrijfwijze hiervoor is V = {(x,y)}. Heel belangrijk om dit telkens erbij te schrijven. Leerkrachten trekken hiervoor punten af bij een test of examen.

Vraagstukken oplossen met eerstegraadsvergelijkingen

Naast het uitleggen van de vier methoden lost Sjoert ook nog een paar vraagstukken op dankzij eerstegraadsvergelijkingen. Heel interessant!

Na het volgen van deze lestrajecten heeft het oplossen van een stelsel geen geheimen meer voor jou. Nog op zoek naar uitleg over andere leerstof? Bekijk dan zeker eens het leerstofoverzicht van WeZooz Academy. Want denk eraan: LOL (Learning On-Line)!

 POPULAIRSTE LESTRAJECTEN 

• STELSELS OPLOSSEN - DEEL 1
• STELSELS OPLOSSEN - DEEL 2
• STELSELS OPLOSSEN - DEEL 3: VRAAGSTUKKEN