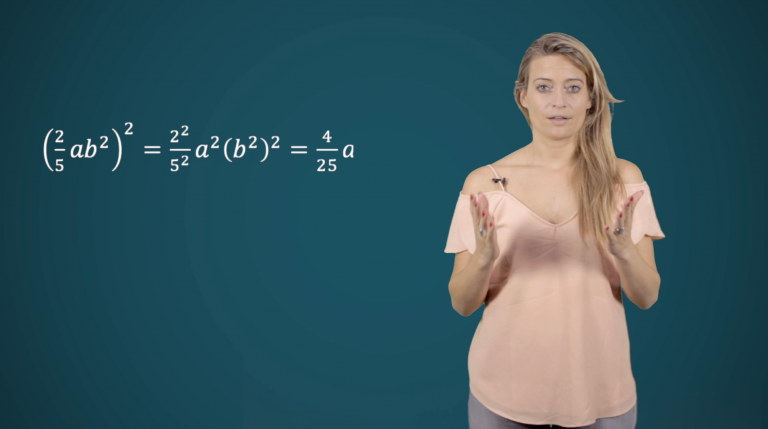Wiskunde 1ste graad A
Veeltermen 1ste graad A
Veeltermen zijn combinaties van getallen en letters in de getallenleer in de wiskunde. Hoe herken je veeltermen? Wat als je ze moet berekenen of herleiden? Naast de verschillende bewerkingen leer je ook over de merkwaardige producten!
Veeltermen
Als je dacht dat de getallenleer in de wiskunde alleen maar over getallen ging, heb je het mis. Eéntermen en veeltermen zijn een belangrijk onderdeel van getallenleer. Het zijn eigenlijk combinaties van getallen én letters. In dit hoofdstuk kan je leren hoe je veeltermen herkent, hoe je ze moet berekenen en hoe je ze kan herleiden. We wijden je bovendien in in de magische wereld van de merkwaardige producten.
Wat is een veelterm?
In de vorige hoofdstukken hebben we al gezien dat er in de wiskunde heel vaak moeilijke of vreemde woorden gebruikt worden voor dingen die achteraf eigenlijk simpel blijken te zijn. Zo is het ook bij ééntermen en veeltermen. Een éénterm is gewoon een vermenigvuldiging van een getal en een letter. En een veelterm is gewoon een optelling of een aftrekking van meerdere ééntermen. Zo simpel is het!
Getalwaarde veelterm
Als je éénmaal weet wat een veelterm is, kan je er ook mee gaan spelen en experimenteren. Zo kan je bijvoorbeeld de getalwaarde van een veelterm berekenen. En hiervoor bestaan er heel wat trucjes. Eigenlijk komt het erop neer om de letters in een veelterm te vervangen door de gegeven waarden, waardoor je een reeks van bewerking krijgt die je kan uitrekenen. Hiervoor pas je de juiste volgorde van bewerkingen toe zoals we eerder hebben gezien.
Veeltermen optellen en veeltermen aftrekken
Je kan ééntermen ook optellen en aftrekken. Dat is op zich niet moeilijk, maar je moet dan wel even snappen wat het betekent als we zeggen dat twee ééntermen gelijksoortig zijn. Liesbeth verduidelijkt het voor jou in een interessante online lesvideo. In de volgende stap leggen we je dan uit hoe je eenvoudige veeltermen optelt en aftrekt.
Veeltermen vermenigvuldigen
Ook voor het vermenigvuldigen van veeltermen bestaan er een aantal richtlijnen. In ons stappenplan laten we je zien dat je eerst de coëfficiënten moet vermenigvuldigen en vervolgens de lettergedeelten. Voor dit laatste spreken we af dat we de letters in alfabetische volgorde noteren.
Machten van eentermen
In ons hoofdstuk Machten en vierkantswortels kan je ontdekken wat de term ‘machten’ in de wiskunde betekent. Bij een machtsverheffing is er altijd sprake van een grondtal en een exponent. Als je de macht van een éénterm wil berekenen, moet je elke factor tot die macht verheffen. Je vermenigvuldigt dan eerst de coëfficiënten met elkaar en dan de lettergedeeltes.
Merkwaardige producten
Wat zijn merkwaardig producten behalve een merkwaardige naam? Met deze vraag komen we dichter en dichter bij het échte werk. Wiskunde voor gevorderden? Misschien wel, maar wij leggen het snel en eenvoudig uit zodat iedereen het snapt. Voor we je echt vertellen wat merkwaardige producten zijn moeten we eerste even verduidelijken wat toegevoegde tweetermen zijn. Eigenlijk zijn merkwaardige producten gewoon het product van toegevoegde tweetermen.
Kwadraat tweeterm
En we zijn niet meer te stoppen nu. We leggen je ook snel en simpel het kwadraat van een tweeterm uit. Een tweeterm is een som of verschil van twee ééntermen. Om tot de juiste formule te komen van het kwadraat van een tweeterm, starten we van de oppervlakte van een vierkant. Dat zal ons helpen om de formule te ontdekken van het kwadraat van een tweeterm.
Veeltermen herleiden
Veeltermen herleiden betekent eigenlijk het eenvoudiger schrijven van ingewikkelde bewerkingen met veeltermen. Hiervoor gebruik je alles wat je geleerd hebt over de eigenschappen en de volgorde van bewerkingen en over veeltermen.